問題 <R3年上期 午後問2>
直径 2.6mm、長さ 20m の銅導線と抵抗値が最も近い同質の銅導線は。
<解答の選択肢>
- 断面積 8mm2、長さ 40m
- 断面積 8mm2、長さ 20m
- 断面積 5.5mm2、長さ 40m
- 断面積 5.5mm2、長さ 20m
【出典:令和3年度第ニ種電気工事士筆記試験上期-午後問2】
抵抗は、抵抗[Ω] = 抵抗率×長さ/断面積 で計算できる。直径 2.6mm の銅導線の断面積は 約 5.3mm2 。したがって、抵抗値が最も近いのは、選択肢4
類似問題
・R3年下期-午後問2
・R3年下期-午前問2
・R3年上期-午後問2
・R2年下期-午後問2
・R2年下期-午前問2
同じ年度の問題
・前の問題(問1)
・次の問題(問3)
・令和3年度上期-午後問題一覧
解法と解説
方針
銅線の抵抗・抵抗率・断面積・長さの関係を表す問題は、過去6回で5回出題されている合格の必須項目。基本となる公式を1つマスターすべし。
ふくラボ流攻略法
銅線(導線)の抵抗 R は、抵抗率 ρ、長さ L 、断面積 S を使って次の公式で求めることができる。
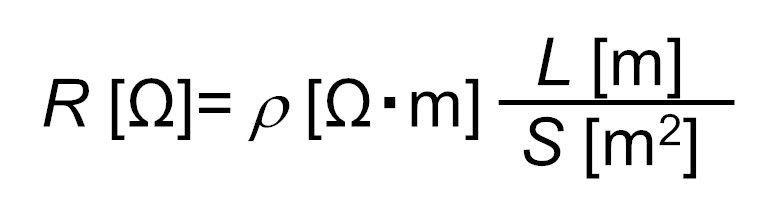
注意点は、長さと断面積とも [m] を基本としている点。
問題文には「同質」の銅導線と書かれているので、抵抗率 ρ は等しい。ということは、残る L/S が等しい(近い)値の選択肢が正解となる。
まず、直径 2.6mm の銅線の断面積 S を求めると
S = π × (半径)2 = π × 1.32 = 5.309… [mm2]
そして、長さ L = 20m。
この銅線と L/S の値が最も近い選択肢を探すと、選択肢4:断面積 5.5mm2、長さ 20m が最も近い。
まとめ
銅線の抵抗・抵抗率・断面積・長さの関係を表す問題は、過去6回で5回出題されている合格の必須項目。基本となる公式を1つマスターすべし。
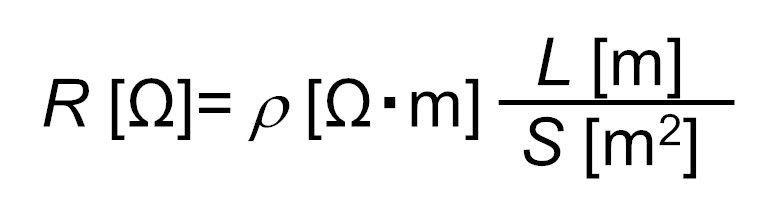
類似問題
・R3年下期-午後問2
・R3年下期-午前問2
・R3年上期-午後問2
・R2年下期-午後問2
・R2年下期-午前問2
解説
・銅線の抵抗の解説
同じ年度の問題
・前の問題(問1)
・次の問題(問3)
・令和3年度上期-午後問題一覧