【電気工事士２種筆記】三相３線式回路の断線前後の電圧(R3年度上期-午前問5)

問題＜R3年上期午前問5＞
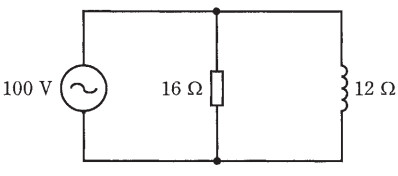
図のような三相３線式 200V の回路で、c-o間の抵抗が断線した。断線前と断線後の a-o間の電圧 V の値 [V] の組合せとして、正しいものは

＜解答の選択肢＞

【出典：令和３年度第ニ種電気工事士筆記試験上期-午前問5】

答えはこちら
断線前はスター結線負荷だから、１相分の抵抗両端の電圧は 200/(√3)=116[V]。断線後は、200V電源に抵抗値の等しい抵抗が２つ直列接続されているから、抵抗１つ両端の電圧は 100V。正しい組み合わせは選択肢２

解法と解説

この問題は、三相回路の断線という珍しいタイプ。
ただ、三相交流回路の線間電圧に関連する問題は、過去６回で４回出題の合格の必須項目。次の重要ポイントを押さえたあと、断線の問題も解けるようにしよう。

スター結線の線間電圧 [V] = √3 × 相電圧 [V]

三相交流回路スター結線の相電圧と線間電圧を図示すると、

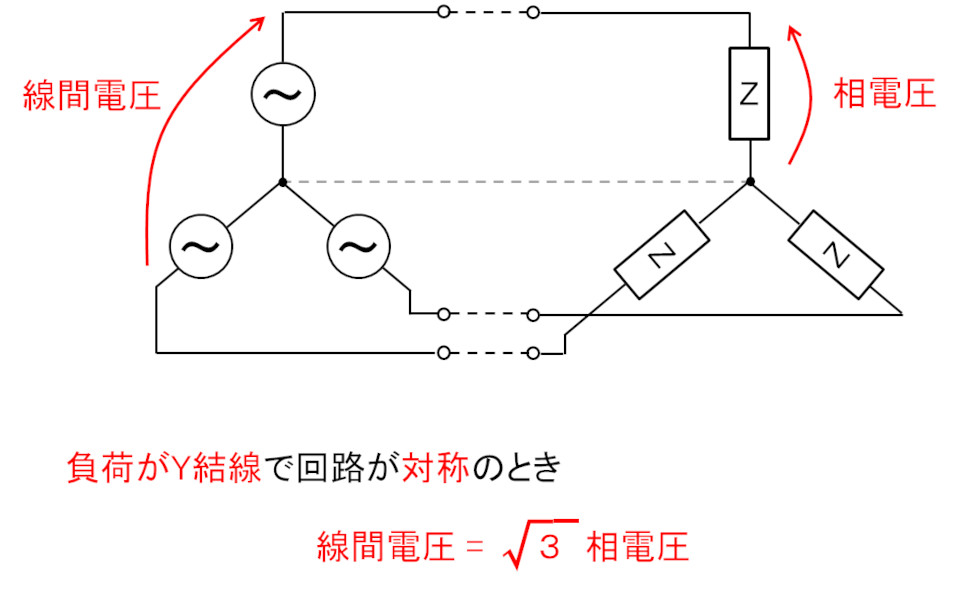
図中にも書いてある通り、(負荷が)Y結線で回路が対称(それぞれの負荷が等しい)とき、次の関係式が成り立つ。

線間電圧 [V] = √3 × 相電圧 [V]

問題文の回路はY結線で、３つの負荷はいずれも R と記述されており、等しい、つまり対称な回路。

したがって、１つの抵抗 R にかかる電圧 = 相電圧は

相電圧 V_P = 200 / √3 = 115.4… [V]

次、問題文の図のように c-o 間の抵抗が断線すると、この抵抗および電路は回路に存在しないことになる。

この状況を、分かりやすいように電源側に Y結線電源を描画して示すと、次のようになる。

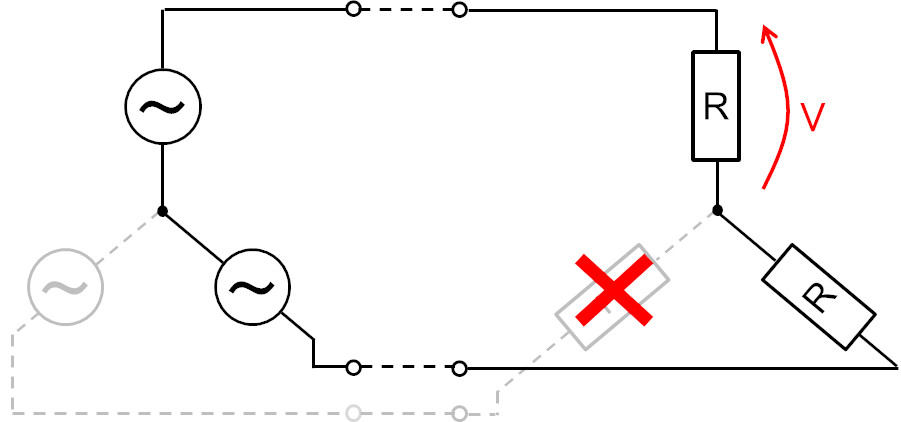
つまり、交流 200V 電源に、大きさの等しい負荷 R が 2個直列に接続されている回路である。

したがって、断線後の V の大きさは 200V の半分、100V となる。

三相交流回路で負荷がY結線のとき、線間電圧に関連する重要ポイントは、

線間電圧 [V] = √3 × 相電圧 [V]